Perhaps when someone stepped on the mine that is responsible for the Big Bang set in motion conditions for life that dictate certain realities. Realities which caused systems in the Honorverse to form and coalesce exactly as they did. At any rate, there appears to be many a similarity which suggest itself. Do forgive the length, as sometimes form must really follow function.
Enter Conway's Game of Life.
The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970.
The "game" is a zero-player game, meaning that its evolution is determined by its initial state, requiring no further input. One interacts with the Game of Life by creating an initial configuration and observing how it evolves, or, for advanced "players", by creating patterns with particular properties. The Game has been reprogrammed multiple times in various coding languages.
Rules
The universe of the Game of Life is an infinite two-dimensional orthogonal grid of square cells, each of which is in one of two possible states, alive or dead, or "populated" or "unpopulated". Every cell interacts with its eight neighbours, which are the cells that are horizontally, vertically, or diagonally adjacent. At each step in time, the following transitions occur:
1. Any live cell with fewer than two live neighbours dies, as if caused by underpopulation.
2. Any live cell with two or three live neighbours lives on to the next generation.
3. Any live cell with more than three live neighbours dies, as if by overpopulation.
4. Any dead cell with exactly three live neighbours becomes a live cell, as if by reproduction.
The initial pattern constitutes the seed of the system. The first generation is created by applying the above rules simultaneously to every cell in the seed—births and deaths occur simultaneously, and the discrete moment at which this happens is sometimes called a tick (in other words, each generation is a pure function of the preceding one). The rules continue to be applied repeatedly to create further generations.
Origins
Conway was interested in a problem presented in the 1940s by mathematician John von Neumann, who attempted to find a hypothetical machine that could build copies of itself and succeeded when he found a mathematical model for such a machine with very complicated rules on a rectangular grid. The Game of Life emerged as Conway's successful attempt to drastically simplify von Neumann's ideas.
The game made its first public appearance in the October 1970 issue of Scientific American, in Martin Gardner's "Mathematical Games" column. From a theoretical point of view, it is interesting because it has the power of a universal Turing machine: that is, anything that can be computed algorithmically can be computed within Conway's Game of Life. Gardner wrote:
- The game made Conway instantly famous, but it also opened up a whole new field of mathematical research, the field of cellular automata ... Because of Life's analogies with the rise, fall and alterations of a society of living organisms, it belongs to a growing class of what are called "simulation games" (games that resemble real life processes).
Ever since its publication, Conway's Game of Life has attracted much interest, because of the surprising ways in which the patterns can evolve. Life provides an example of emergence and self-organization. Scholars in various fields, such as computer science, physics, biology, biochemistry, economics, mathematics, philosophy, and generative sciences have made use of the way that complex patterns can emerge from the implementation of the game's simple rules[citation needed]. The game can also serve as a didactic analogy, used to convey the somewhat counterintuitive notion that "design" and "organization" can spontaneously emerge in the absence of a designer. For example, philosopher and cognitive scientist Daniel Dennett has used the analogue of Conway's Life "universe" extensively to illustrate the possible evolution of complex philosophical constructs, such as consciousness and free will, from the relatively simple set of deterministic physical laws, which might govern our universe.
The popularity of Conway's Game of Life was helped by its coming into being just in time for a new generation of inexpensive computer access which were being released into the market. The game could be run for hours on these machines, which would otherwise have remained unused at night. In this respect, it foreshadowed the later popularity of computer-generated fractals. For many, Life was simply a programming challenge: a fun way to use otherwise wasted CPU cycles. For some, however, Life had more philosophical connotations. It developed a cult following through the 1970s and beyond; current developments have gone so far as to create theoretic emulations of computer systems within the confines of a Life board.
Conway chose his rules carefully, after considerable experimentation, to meet these criteria:
1. There should be no explosive growth.
2. There should exist small initial patterns with chaotic, unpredictable outcomes.
3. There should be potential for 3. von Neumann universal constructors.
4. The rules should be as simple as possible, whilst adhering to the above constraints.
Examples of patterns
The earliest interesting patterns in the Game of Life were discovered without the use of computers. The simplest static patterns ("still lifes") and repeating patterns ("oscillators"—a superset of still lifes) were discovered while tracking the fates of various small starting configurations using graph paper, blackboards, physical game boards (such as Go) and the like. During this early research, Conway discovered that the R-pentomino failed to stabilize in a small number of generations. In fact, it takes 1103 generations to stabilize, by which time it has a population of 116 and has fired six escaping gliders (these were the first gliders ever discovered).
Many different types of patterns occur in the Game of Life, including still lifes, oscillators, and patterns that translate themselves across the board, including the glider, discovered by Richard K. Guy in 1970, and several kinds of spaceships. Some frequently occurring examples of these three classes are shown below, with live cells shown in black, and dead cells shown in white.
Still lifes:
A still life is a pattern that does not change from one generation to the next. A still life can be thought of as an oscillator with unit period.
Classifications
A pseudo still life consists of two or more adjacent islands (connected components) which can be partitioned (either individually or as sets) into non-interacting subparts, which are also still lifes. This compares with a strict still life, which may not be partitioned in this way. A strict still life may have only a single island, or it may have multiple islands that depend on one another for stability, and thus cannot be decomposed. The distinction between the two is not always obvious, as a strict still life may have multiple connected components all of which are needed for its stability. However, it is possible to determine whether a still life pattern is a strict still life or a pseudo still life in polynomial time by searching for cycles in an associated skew-symmetric graph.
pseudo-still
 strict still
strict still
Examples:
There are many naturally occurring still lifes in Conway's Game of Life. A random initial pattern will leave behind a great deal of debris, containing small oscillators and a large variety of still lifes.
The most common still life (i.e. that most likely to be generated from a random initial state) is the block. A pair of blocks placed side-by-side (or bi-block) is the simplest pseudo still life. Blocks are used as components in many complex devices, an example being the Gosper glider gun.
block

The second most common still life is the hive (or beehive). Hives are frequently created in (non-interacting) sets of four, in a formation known as a honey farm.
hive
 honey farm
honey farm
The third most common still life is the loaf. Loaves are often found together in a pairing known as a bi-loaf. Bi-loaves themselves are often created in a further (non-interacting) pairing known as a bakery. Two bakeries can extremely rarely form next to each other, forming a set of four loaves known as a tetraloaf alongside two more bi-loafs.
loaf
 bakery
bakery
A tub consists of four live cells placed in a diamond shape around a central dead cell. Placing an extra live cell diagonally to the central cell gives another still life, known as a boat. Placing a further live cell on the opposite side gives yet another still life, known as a ship. A tub, a boat or a ship can be extended by adding a pair of live cells, to give a barge, a long-boat or a long-ship respectively. This extension can be repeated indefinitely, to give arbitrarily large structures.
From left: tub, barge, long barge, etc.
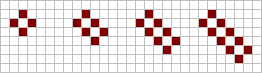
From left: boat, long boat, etc.

From left: ship, long ship, etc.

Eaters (Do expansionistic polities, like the PRH and the SL remind you of eaters?)
Still lifes can be used to modify or destroy other objects. A still life is called an eater when it can be used to absorb some other pattern (often a glider, spaceship, or the debris from a more complicated reaction) and returns to its original state after the collision. Many examples exist, with the most notable being the fish-hook (Also known as eater 1), which is capable of absorbing several types of spaceship. A similar device is the reflector, which alters the direction of an incoming spaceship. Oscillators with similar properties may also be called eaters or reflectors, but are more difficult to apply as they must be synchronized to the pattern they modify. Still life eaters and reflectors, on the other hand, work correctly regardless of the timing of the pattern they modify, as long as successive reactions occur with enough separation in time to allow the eater or reflector to recover its original shape.
fish hook eater (symbolic of the shape of Haven)

eater2 (symbolic of the larger SL)
Smaller patterns were later found that also exhibit infinite growth. All three of the following patterns grow indefinitely: the first two create one "block-laying switch engine" each, while the third creates two. The first has only 10 live cells (which has been proven to be minimal). The second fits in a 5 × 5 square. The third is only one cell high: See Site.
____There is even a notion of maximum density_____

Oscillators
blinker
toad
beacon
pulsar
pentadecathlon
Now isn't this interesting...
Spaceship
Lightweight spaceship
Later discoveries included other "guns", which are stationary, and which shoot out gliders or other spaceships; "puffers", which move along leaving behind a trail of debris; and "rakes", which move and emit spaceships. Gosper also constructed the first pattern with an asymptotically optimal quadratic growth rate, called a "breeder", or "lobster", which worked by leaving behind a trail of guns.
It is possible for gliders to interact with other objects in interesting ways. For example, if two gliders are shot at a block in just the right way, the block will move closer to the source of the gliders. If three gliders are shot in just the right way, the block will move farther away. This "sliding block memory" can be used to simulate a counter. It is possible to construct logic gates such as AND, OR and NOT using gliders. It is possible to build a pattern that acts like a finite state machine connected to two counters. This has the same computational power as a universal Turing machine, so the Game of Life is theoretically as powerful as any computer with unlimited memory and no time constraints: it is Turing complete.
Furthermore, a pattern can contain a collection of guns that fire gliders in such a way as to construct new objects, including copies of the original pattern. A "universal constructor" can be built which contains a Turing complete computer, and which can build many types of complex objects, including more copies of itself.
Undecideability: The Verge
Many patterns in the Game of Life eventually become a combination of still lifes, oscillators and spaceships; other patterns may be called chaotic. A pattern may stay chaotic for a very long time until it eventually settles to such a combination.
It can be asked whether Life is decidable: whether an algorithm exists, so that given an "initial" pattern and a "later" pattern, the algorithm can tell whether, starting with the initial pattern, the later pattern is ever going to appear. This turns out to be impossible: no such algorithm exists. This is in fact a corollary of the halting problem.
Indeed, since Life includes a pattern that is equivalent to a UTM (universal Turing machine), this "deciding" algorithm, if it existed, could have been used to solve the halting problem, by taking the initial pattern as the one corresponding to a UTM+input and the later pattern as the one corresponding to a halting state of the machine with an empty tape (as one can modify the Turing machine to always erase the tape before halting). However the halting problem is provably undecidable and so such an algorithm does not exist.
It also follows that some patterns exist that remain chaotic forever: otherwise one could just progress the game sequentially until a non-chaotic pattern emerges, and then easily compute whether the later pattern is going to appear.
Self-replication: The MAlign
On May 18, 2010, Andrew J. Wade announced a self-constructing pattern dubbed Gemini which creates a copy of itself while destroying its parent. This pattern replicates in 34 million generations, and uses an instruction tape made of gliders which oscillate between two stable configurations made of Chapman-Greene construction arms. These, in turn, create new copies of the pattern, and destroy the previous copy. Gemini is also a spaceship, and is the first spaceship constructed in the Game of Life that is a knightship, which is a spaceship that is neither orthogonal nor purely diagonal.
On November 23, 2013, Dave Greene built the first replicator in Conway's Game of Life that creates a complete copy of itself, including the instruction tape.
In December 2015, diagonal versions of the Gemini were built.
Iteration
From most random initial patterns of living cells on the grid, observers will find the population constantly changing as the generations tick by. The patterns that emerge from the simple rules may be considered a form of beauty. Small isolated subpatterns with no initial symmetry tend to become symmetrical. Once this happens, the symmetry may increase in richness, but it cannot be lost unless a nearby subpattern comes close enough to disturb it. In a very few cases the society eventually dies out, with all living cells vanishing, though this may not happen for a great many generations. Most initial patterns eventually "burn out", producing either stable figures or patterns that oscillate forever between two or more states; many also produce one or more gliders or spaceships that travel indefinitely away from the initial location. Because of the nearest-neighbour based rules, no "information" can travel through the grid at a greater rate than one cell per unit time, so this velocity is said to be the cellular automaton speed of light and denoted c.
Glider:
The glider is a pattern that travels across the board in Conway's Game of Life. It was first discovered by Richard K. Guy in 1970, while John Conway's group was attempting to track the evolution of the R-pentomino. Gliders are the smallest spaceships, and they travel diagonally at a speed of c/4. The glider is often produced from randomly generated starting configurations. John Conway has remarked that he wishes he hadn't called it the glider. The game was developed before the widespread use of interactive computers, and after seeing it animated, he feels the glider looks more like an ant walking across the plane.

Importance
Gliders are important to the Game of Life because they are easily produced, can be collided with each other to form more complicated objects, and can be used to transmit information over long distances. For instance, eight gliders can be positioned so that they collide to form a Gosper glider gun. Glider collisions designed to result in certain patterns are also called glider syntheses.
A single gosper glider gun creating gliders.

Patterns like blocks, beehives, blinkers, traffic lights, even the uncommon Eater, can be synthesized with just two gliders. It takes three gliders to build the three other basic spaceships, and even the pentadecathlon.
Some patterns require a very large number (scores, even hundreds) of glider collisions; some oscillators, exotic spaceships, puffer trains, guns, etc. Whether the construction of an exotic pattern from gliders can possibly mean it can occur naturally, is still conjecture.
Gliders can also be collided with other patterns with interesting results. For example, if two gliders are shot at a block in just the right way, the block will move closer to the source of the gliders. If three gliders are shot in just the right way, the block will move farther away. This "sliding block memory" can be used to simulate a counter, which would be modified by firing gliders at it. It is possible to construct logic gates such as AND, OR and NOT using gliders. One may also build a pattern that acts like a finite state machine connected to two counters. This has the same computational power as a universal Turing machine, so, using the glider, the Game of Life is theoretically as powerful as any computer with unlimited memory and no time constraints: it is Turing complete.
The "pulsar" is the most common period 3 oscillator. The great majority of naturally occurring oscillators are period 2, like the blinker and the toad, but oscillators of many periods are known to exist, and oscillators of periods 4, 8, 14, 15, 30 and a few others have been seen to arise from random initial conditions. Patterns called "Methuselahs" can evolve for long periods before stabilizing, the first-discovered of which was the R-pentomino. "Diehard" is a pattern that eventually disappears (rather than merely stabilizing) after 130 generations, which is conjectured to be maximal for patterns with seven or fewer cells. "Acorn" takes 5206 generations to generate 633 cells including 13 escaped gliders.
Methuselah (The Malign?)

Variations
Since Life's inception, new similar cellular automata have been developed. The standard Game of Life is symbolized as "B3/S23": A cell is "Born" if it has exactly 3 neighbours, "Survives" if it has 2 or 3 living neighbours; it dies otherwise. The first number, or list of numbers, is what is required for a dead cell to be born. The second set is the requirement for a live cell to survive to the next generation. Hence "B6/S16" means "a cell is born if there are 6 neighbours, and lives on if there are either 1 or 6 neighbours". Cellular automata on a two-dimensional grid that can be described in this way are known as Life-like cellular automata. Another common Life-like automaton, Highlife, is described by the rule B36/S23, because having 6 neighbours, in addition to the original game's B3/S23 rule, causes a birth. HighLife is best known for its frequently occurring replicators. Additional Life-like cellular automata exist, although the vast majority of them produce universes that are either too chaotic or too desolate to be of interest.
Does the rules for life cropping up in the Honorverse follow similar patterns or notions?
This has been composed using one two different sites as a purely cerebral exercise. Do share your natural, instinctual insight.
Video.
.















